Algorithms 101: Basic Data Structures Pt. 2
This article will cover another bunch of must-know data structures, such as heaps, priority queues, associative arrays and hashes. Source code of examples used in this article is available in git repo.
Heaps
Heap is a tree-like data structure satisfying the following property: the key of parent node is ordered with respect of the key of child node. According to the order, heaps can be divided into max heaps (parent key is greater than the chilld's one) and min heaps (parent key is lesser than the child's one). According to the structure of an underlying tree heaps can be binary, d-ary, binomial, fibonacci and many others. The following interface is used to represent heaps:
package com.dancingrobot84.algorithms.datastructures;
public interface Heap<T extends Comparable<? super T>> {
/** Get top item without removing it from heap **/
public T peek();
/** Get top item and remove it from heap **/
public T pop();
/** Return number of items in heap **/
public int size();
/** Insert new item into heap **/
public void insert(T item);
}
Heaps are usually used to implement priority queues, which are used in some graph algorithms (Prim, Dijkstra). Heapsort sorting algorithm is another example of heap's usage.
AFAIK there is no particular implementation of heap as data structure in Java
and C++ languages. However, there is std::make_heap function in C++ standard
library which rearranges elements in given container in a way that they form
a heap. As for Java, there is PriorityQueue class which uses heap under the
hood.
Binary min heap implementation
Idea: this implementation does not have explicit tree structure. Instead,
array is used to store nodes. Index of given node is used to identify its parent
and children (getParent, getLeftChild and getRightChild methods). The
image below gives an example of how to store binary heap of 7 items in an array.
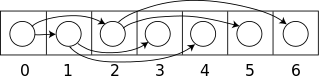
The most important part of heap implementation is methods for maintaining heap
property. In case of binary heap there are two of such methods: bubbleUp and
bubbleDown. bubbleUp compares given element and its parent and if they
violate heap property, exhanges them and moves up the tree. bubbleDown
does the same thing, only for the children of the given element and moves down
the tree. The first method is used to implement insert: we put new item at the
end of an array and run bubbleUp on it in order to put it in its place. The
second method is used to implement popMinimum: we exchange the top item with
the last one and run bubbleDown on the top item in order to put it in its
place.
Now the last thing to do is how to heapify given array efficiently. Naive
approach is to create an empty heap and perform n insertions, which gives us
O(nlog(n)) time and O(n) space. However, it is possible to do it in O(n) time
and O(1) space using bubbleDown method: just iterate over the array in reverse
order and run bubbleDown on each item.
package com.dancingrobot84.algorithms.datastructures.impl;
import com.dancingrobot84.algorithms.datastructures.Heap;
import com.dancingrobot84.algorithms.util.ArraysExt;
public class BinaryHeap<T extends Comparable<? super T>> implements Heap<T> {
public static <T extends Comparable<? super T>> Heap<T> emptyWithCapacity(int capacity) {
return new BinaryHeap<T>(capacity);
}
public static <T extends Comparable<? super T>> Heap<T> fromArray(T[] array) {
return new BinaryHeap<T>(array);
}
@Override
public T peek() {
assert size() > 0 : "Heap is empty";
return array[0];
}
@Override
public T pop() {
T min = peek();
ArraysExt.swap(array, 0, lastPos);
lastPos -= 1;
bubbleDown(0);
return min;
}
@Override
public int size() {
return lastPos + 1;
}
@Override
public void insert(T item) {
assert size() < capacity() : "Heap is full";
lastPos += 1;
array[lastPos] = item;
bubbleUp(lastPos);
}
public int capacity() {
return array.length;
}
private final T[] array;
private int lastPos;
@SuppressWarnings("unchecked")
private BinaryHeap(int capacity) {
array = (T[])new Comparable[Math.max(capacity, 0)];
lastPos = -1;
}
private BinaryHeap(T[] originalArray) {
array = originalArray;
lastPos = array.length - 1;
for (int i = lastPos; i >= 0; i--) {
bubbleDown(i);
}
}
private void bubbleDown(int pos) {
if (pos < 0 || pos > lastPos) {
return;
}
int minPos = pos;
int leftPos = getLeftChild(pos);
if (leftPos <= lastPos && array[minPos].compareTo(array[leftPos]) == 1) {
minPos = leftPos;
}
int rightPos = getRightChild(pos);
if (rightPos <= lastPos && array[minPos].compareTo(array[rightPos]) == 1) {
minPos = rightPos;
}
if (minPos != pos) {
ArraysExt.swap(array, pos, minPos);
bubbleDown(minPos);
}
}
private void bubbleUp(int pos) {
int parentPos = getParent(pos);
if (pos < 0 || pos > lastPos || parentPos < 0 || parentPos > lastPos) {
return;
}
if (array[parentPos].compareTo(array[pos]) == 1) {
ArraysExt.swap(array, parentPos, pos);
bubbleUp(parentPos);
}
}
private int getLeftChild(int parentPos) {
return 2 * parentPos + 1;
}
private int getRightChild(int parentPos) {
return 2 * parentPos + 2;
}
private int getParent(int childPos) {
childPos = childPos % 2 == 0 ? childPos - 2 : childPos - 1;
return childPos / 2;
}
}
isEmpty and getMinimum have O(1) time complexity. Because both bubbleUp
and bibbleDown take O(nlog(n)) time, insert and popMinimum methods have
the same time complexity. As for Heap(int[]) ctor: though it is just n runs
of bubbleDown which sholud give us O(nlog(n)) time, actually, it works
faster than that, because most of heapification takes place in lower levels.
Complete proof of its time complexity can be found on
Wikipedia.
Priority Queues
Priority queue is abstract data structure similar to stack or queue, but the order of items retrieving in it depends on items' priorities. Usually item with the highest priority is served first.
Priority queues applicable in many popular algorithms: Dijkstra, Prim, Huffman
encoding, etc. There are implementations of priority queues in C++ and Java:
std::priority_queue and PriorityQueue classes respectively.
Implementation of priority queue using binary min heap
No additional comments as implementation is quite straightforward.
package com.dancingrobot84.algorithms.datastructures;
public class PriorityQueue<T extends Comparable<? super T>> {
private final Heap<T> heap;
public PriorityQueue(int capacity) {
heap = BinaryHeap.<T>emptyWithCapacity(capacity);
}
public void insert(T item) {
heap.insert(item);
}
public T pop() {
return heap.pop();
}
}
Associative arrays
Associative array or map is an abstract data structure. It stores key-value pairs in such a way, that each possible key appears only once. To describe associative array the following interface is used:
package com.dancingrobot84.algorithms.datastructures;
public interface Map<K extends Comparable<? super K>, V> {
/** Return value associated with a key or null otherwise **/
public V get(K key);
/** Insert value into the map under specified key or rewrite if such key already exists **/
public void put(K key, V value);
}
Associative arrays are applicable in great variaties of computer tasks: removing duplicates, counting items, etc. There are even specials databases called "key-value storage" which store key-value pairs either in memeory or on disk (Redis, Memcached, etc).
Hash Tables
Hash table is one of data structures implementing associative array. It uses
array to store key-value pairs and special hash function to compute index of
particular pair by its key. Usually, for implementation of map it performs
better than binary search tree (both put and get work in O(1) amortized
comparing to O(log(n)) in BST), but it is highly dependent on choosing the
right hash function, load factor and collision resolution method.
Hash tables are used to implement maps, sets, database indexes and caches. They
are available in almost any modern programming language. Some languages provide
them as syntactic construct (Python, Ruby), others have specific classes in
standard libraries (std::unordered_map in C++ and HashMap in Java).
Implementation of hash table
Idea: hash table is always implemented as underlying array containing entries. Depending on collision resolution method, entries could be either key-value pairs or their chains. There are several methods for collision resolution; the most popular ones are open adressing and chaining.
Open addressing method implements the following strategy: when collision occurs during insertion, try to find a different place in array for particular key by sequential probing of other places until the free one is found. When searching for a value, pairs are traversed in exactly the same way. There are several ways of choosing which places to look at when searching for the free one; the easiest method, called "linear probing", just looks at the place following the current one.
Chaining method solves the collision problem differently. It stores buckets of pairs in underlying array; when collision occurs, new pair is dropped in associated bucket. When searching for a value, bucket is searched. Usually, buckets are implemented as linked lists of pairs. The implementation below uses this method.
Another important part of hash table implementation is choosing the right hash
function. The main requirement of hash function is uniform distribution of its
values. The uniformity is crucial; otherwise the number of collisions rises
causing bad performance of hash table. Though, for particular implementation
this condition can be loosen to uniformity at specific sizes. The implementation
below relies on hashCode function of Java's Object for simplicity and
performs no additional hashing. It may affect performance as programmers writing
classes are not obliged to guarantee uniformity of hashCode.
As the number of items in hash table grows, the chance of collision rises too; that's why it is necessary to resize underlying array and re-insert all key-value pairs sometimes. To determine the time for performing this action, load factor indicator is used. It is calculated as the number of key-value pairs inserted divided by the size of underlying array. As for the implementation below, load factor of 0.75 indicates that resizing is needed; the number was chosen manually, though in real world you may want to perform some experiments to choose it more precisely.
package com.dancingrobot84.algorithms.datastructures.impl;
import com.dancingrobot84.algorithms.datastructures.Map;
public class HashMap<K extends Comparable<? super K>, V> implements Map<K, V> {
public static final int DEFAULT_CAPACITY = 2;
public static <K extends Comparable<? super K>, V> Map<K, V> empty() {
return new HashMap<K, V>(DEFAULT_CAPACITY);
}
public static <K extends Comparable<? super K>, V> Map<K, V> emptyWithCapacity(int capacity) {
return new HashMap<K, V>(capacity);
}
@Override
public V get(K key) {
checkKey(key);
Entry<K, V> entry = entries[findIndex(key)];
for (; entry != null; entry = entry.next) {
if (key.compareTo(entry.key) == 0) {
return entry.value;
}
}
return null;
}
@Override
public void put(K key, V value) {
checkKey(key);
int index = findIndex(key);
Entry<K, V> entry = entries[index];
for (; entry != null; entry = entry.next) {
if (key.compareTo(entry.key) == 0) {
entry.value = value;
return;
}
if (entry.next == null) {
break;
}
}
Entry<K, V> newEntry = new Entry<K, V>(key, value);
if (entry == null) {
entries[index] = newEntry;
} else {
entry.next = newEntry;
}
size++;
if (isFull()) {
resize(entries.length * 2);
}
}
private int size;
private Entry<K, V>[] entries;
@SuppressWarnings("unchecked")
private HashMap(int capacity) {
size = 0;
entries = (Entry<K, V>[])new Entry[Math.max(capacity, DEFAULT_CAPACITY)];
}
private static class Entry<K, V> {
public K key;
public V value;
public Entry<K, V> next;
public Entry(K key, V value) {
this.key = key;
this.value = value;
}
}
private void checkKey(K key) {
assert key != null : "Nullary keys are forbidden";
}
private int findIndex(K key) {
return key.hashCode() % entries.length;
}
private boolean isFull() {
return size >= 0.75 * entries.length;
}
@SuppressWarnings("unchecked")
private void resize(int newCapacity) {
Entry<K, V>[] oldEntries = entries;
entries = (Entry<K, V>[])new Entry[newCapacity];
size = 0;
for (int i = 0; i < oldEntries.length; i++) {
for (Entry<K, V> entry = oldEntries[i]; entry != null; entry = entry.next) {
put(entry.key, entry.value);
}
}
}
}
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms